一、求解思想
将大整数表示成多项式;考虑到是字符串,直接用每一位的数字作为多项式的系数A(x),该整数就是多项式在x=10处的值。
用点值表示法表示该多项式,即 Wa=y 。其中W中一行就对应一个x 值, a是一个列向量,对应多项式的系数, y是一个列向量,一行对应一个 x的结果。常规的取点并不能降低时间复杂度。这里我们取n个n次单位复根$w^k_{n}$,$k={0,1,…n-1}$作为x,要求每个单位复根对应的$y=A(x)$值。对于$y_{k}=A(w^k_{n})$,我们根据系数把它拆成偶数部分和奇数部分,即
\[A^0(x)=a_{0}x+a_{2}x+\cdots+a_{n-2}x\] \[A^1(x)=a_{1}x+a_{3}x+\cdots+a_{n-1}x\]利用相消定理可以化成递归的形式: $y_{k}=A(w^k_{n} )=A^0(w^k_{n/2})+w^k_{n}A^1(w^k_{n/2})$ ,进一步利用折半定理可以得到 $y_{k+n/2}=A(w^k_{n} )=A^0(w^k_{n/2})-w^k_{n}A^1(w^k_{n/2}) $。所以我们可以利用递归求出奇数和偶数部分的FFT(divide)结果,再利用上面的公式求出所有的$ y_{k} $(conquer)
求得 A(x) 和B(x)后,把它们对应相乘就得到C(x)。现在我们反过来要求系数。根据矩阵的逆变换我们很容易可以得到逆傅里叶换方法,只需要简单的变个符号,最后再除以n即可。
二、运行结果
具体代码
import math
import random
import string
pi = math.pi
def euler_formula(x):
# 欧拉公式
return complex(math.cos(x), math.sin(x))
def root_w(n, k):
# 单位根
return euler_formula(2 * pi * k / n)
def FFT(a, reverse=False):
# 递归版本FFT;若reverse=True则为逆FFT
n = len(a)
if n == 1:
return a
w_n = root_w(n, 1) if not reverse else root_w(n, -1) # w^1_{n}和w^-1_{n}
w = 1
# divide and conquer
a_even = [a[i] for i in range(0, n, 2)] # 取出偶数位系数a
a_odd = [a[i] for i in range(1, n, 2)] # 取出奇数位系数a
y_even = FFT(a_even, reverse) # 递归对A^0(x)做FFT
y_odd = FFT(a_odd, reverse) # 递归对A^1(x)做FFT
# combine
y = [0] * n
for i in range(0, n//2):
y[i] = y_even[i] + w * y_odd[i] # 根据消去引理
y[i + n//2] = y_even[i] - w * y_odd[i] # 根据折半原理
w = w * w_n
return y
def pad(string, pad_len):
# 将字符串转化为多项式系数,以10作为x,长度为pad_len
return [int(string[i]) if i >=0 else 0 for i in range(len(string)-1, len(string)-pad_len-1, -1)]
def mutiply(string1, string2):
# 取保长度为2的次幂
maxlen = len(string1) if len(string1) > len(string2) else len(string2)
pad_len = 1
while pad_len < maxlen:
pad_len *= 2
pad_len *= 2
# 转化为多项式系数[a]
a1 = pad(string1, pad_len)
a2 = pad(string2, pad_len)
# 用FFT求得A(x)和B(x)
A , B = FFT(a1), FFT(a2)
# 对应相乘求得C(x)
C = [x * y for x, y in zip(A, B)]
# 逆FFT求得系数a
a = FFT(C, reverse=True)
# 取整
a = [int(x.real/pad_len+0.5) for x in a]
# 进位
for i in range(0, len(a)-2):
a[i+1] += a[i] // 10
a[i] = a[i] % 10
# 去掉高位多余的0
pointer = len(a) - 1
while(a[pointer] == 0):
pointer -= 1
if pointer < 0:
return '0'
return ''.join(reversed([str(x) for x in a[:pointer+1]]))
if __name__ == '__main__':
# 随机生成100位的整数,最高位不能为0
string1 = random.sample('123456789',1)[0] + ''.join(map(lambda x:random.choice('0123456789'), range(99)))
string2 = random.sample('123456789',1)[0] + ''.join(map(lambda x:random.choice('0123456789'), range(99)))
print(string1 + ' * '+ string2 + '=' + mutiply(string1, string2))
运行环境
python>=3.6
运行方法
python3 main.py
运行结果
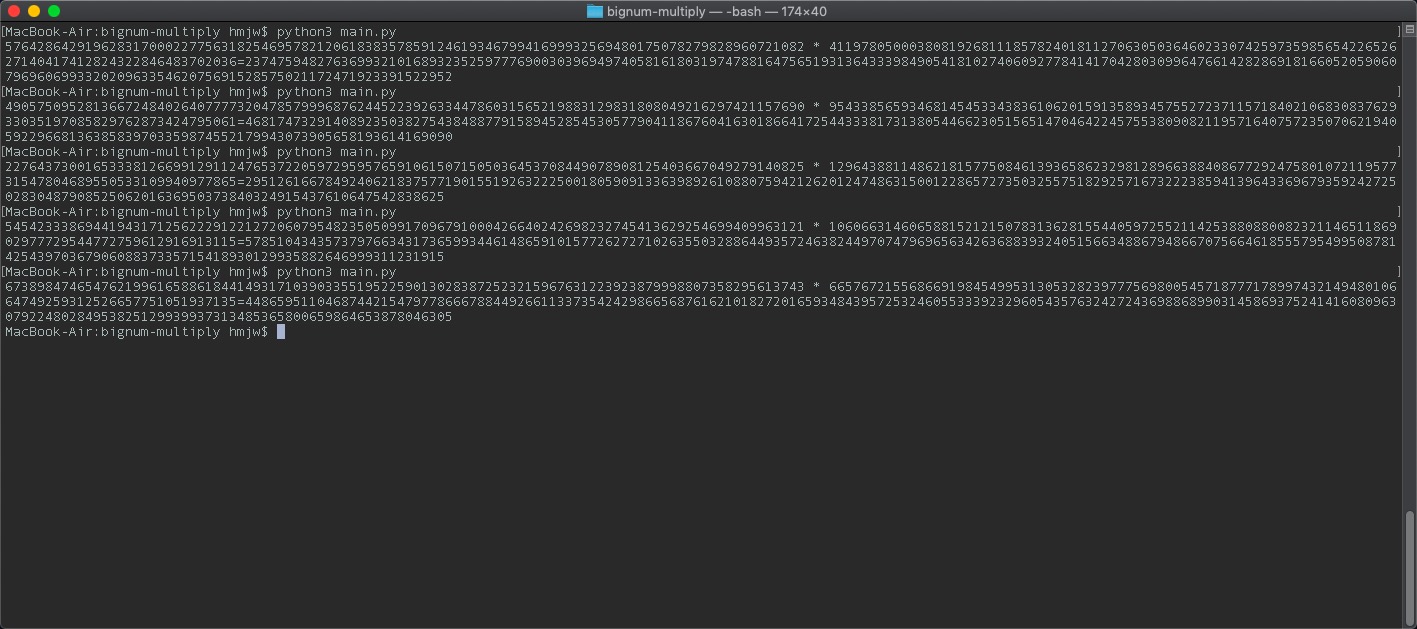
下图是在本地自拟100位乘100位整数的结果:
下图是在Leetcode Multiply Strings测试运行的结果: