无监督学习：AE到VAE

• 参考链接
• 引言
• Deep Auto-Encoder(AE)
• Variational Auto-Encoder(VAE)
  • 从AE的角度来看
  • 从生成模型的角度看
  • KL距离loss推导

参考链接

• 李宏毅机器学习视频

• 变分自编码器（一）：原来是这么一回事

• Tutorial - What is a variational autoencoder?

• Variational Autoencoder: Intuition and Implementation

• Tutorial on Variational AutoEncoders

• Variational autoencoders

下文的大部分图片及资料均来自上述链接。

引言

无监督学习是从无标注的数据中学习数据的统计规律或者说内在结构的机器学习，主要包括聚类、降维、概率估计。无监督学习可以用于数据分析或者监督学习的前处理。

无监督学习使用无标注数据$U = {x_1, x_2, …, x_N}$学习或训练，无监督学习的模型是函数$z = g_{\theta}(z)$，条件概率分布$P_{\theta}(z|x)$，或条件概率分布$P_{\theta}(x|z)$。其中$x \in X$是输入，表示样本；$z \in Z$是输出，表示对样本的分析结果，可以是类别、转换、概率；$\theta$是参数。 (摘自统计学习方法)

Deep Auto-Encoder(AE)

Deep AE是一种用神经网络对数据进行压缩的模型。简单来讲就是我们希望有一个模型(encoder)能将原始的数据（向量）$x$压缩成一个维度小的多的向量$z$，$z$中包含了$x$尽可能完整的重要信息。那么如何得到比较好的$z$或者说我们如何训练这个encoder？我们构造另一个模型(decoder)，输入是$z$，输出为$\hat{x}$，若能从$z$尽可能完整的还原$x$也就是$\hat{x}$和$x$越像，则说明$z$越好。所以AE的模型框架如下。

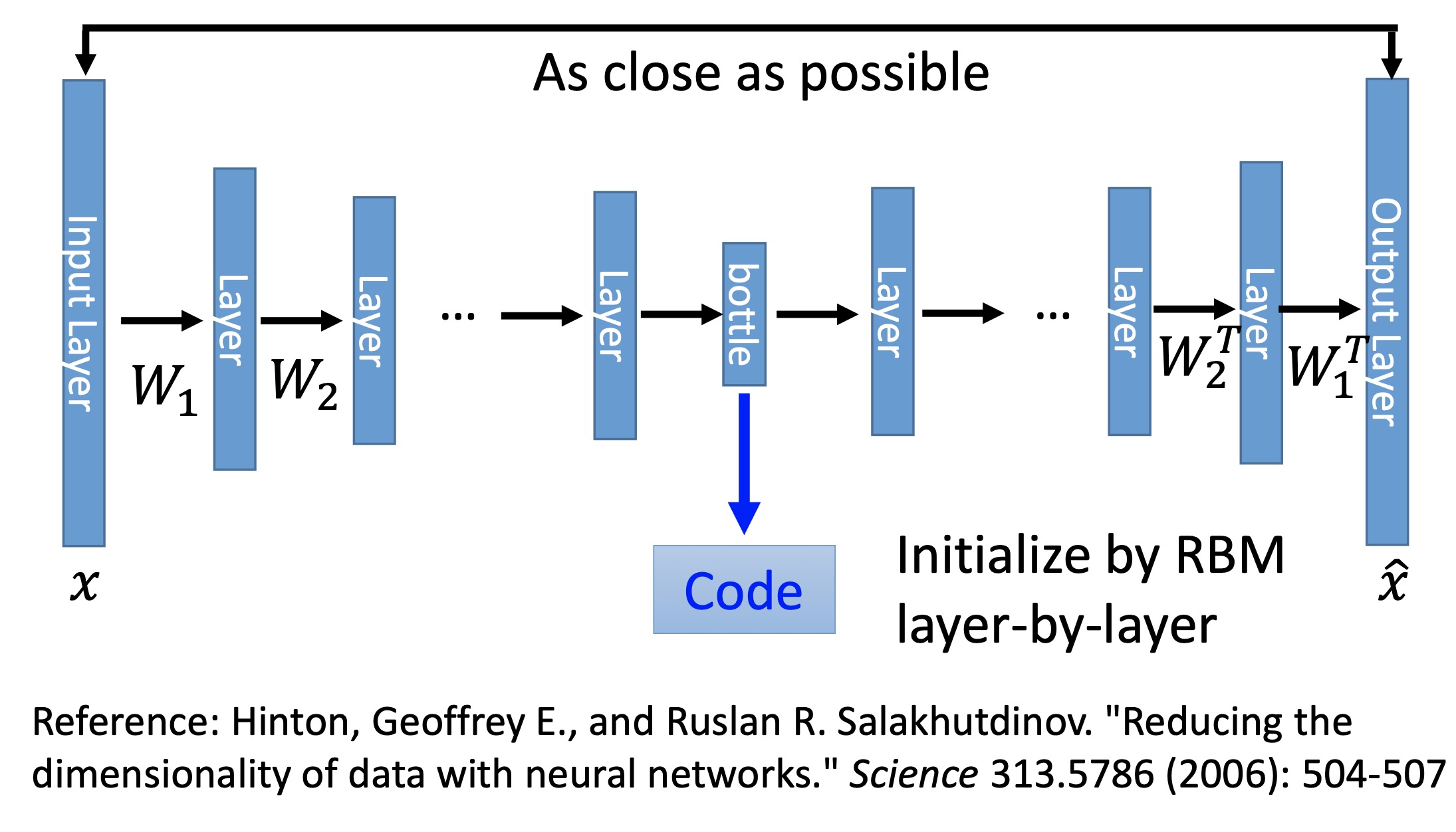
图中的code就是压缩后的信息，其维度要比$x$的维度小得多（如果维度大于等于$x$的维度，那么理论上只要做一个copy操作到code中，其他维度都没有用；维度小就会迫使网络去提取$x$中有用的信息）。code的左侧就是encoder，右侧就是decoder，训练时的reconstruction loss就是$Loss(x, \hat{x})$。

AE有着许许多多应用，不在此赘述。BERT可以看成是一个特殊的AE（De-noising auto-encoder）。输入为一个句子，然后对句子增加一些噪音（mask掉一些词），我们希望模型能尽可能的还原出来原始的句子。

Variational Auto-Encoder(VAE)

从名字可以看出，VAE是AE的变种，所以它大体上仍然遵循AE的框架，通过encoder得到输入$x$的隐变量$z$，再通过decoder将$z$还原成$x$, 如下图：

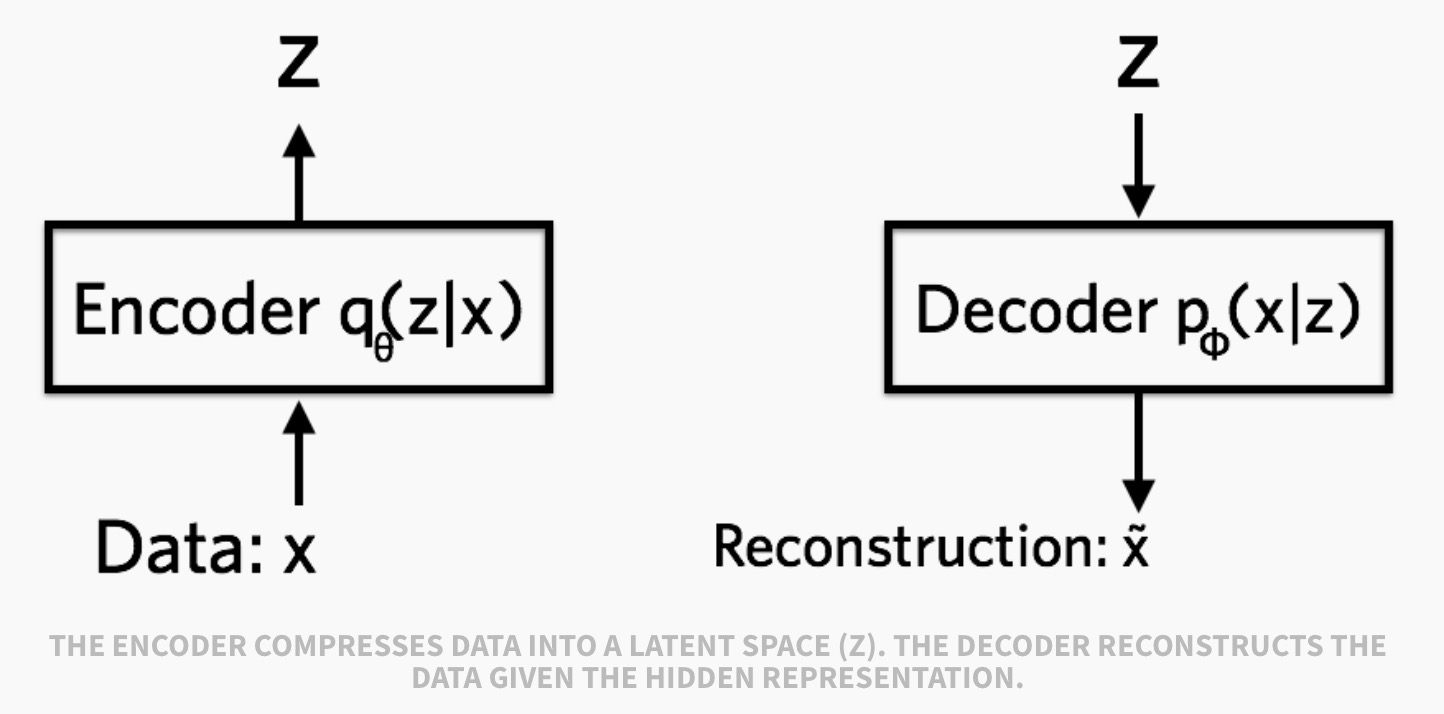
但是具体模型上有两个不同，如下图所示：

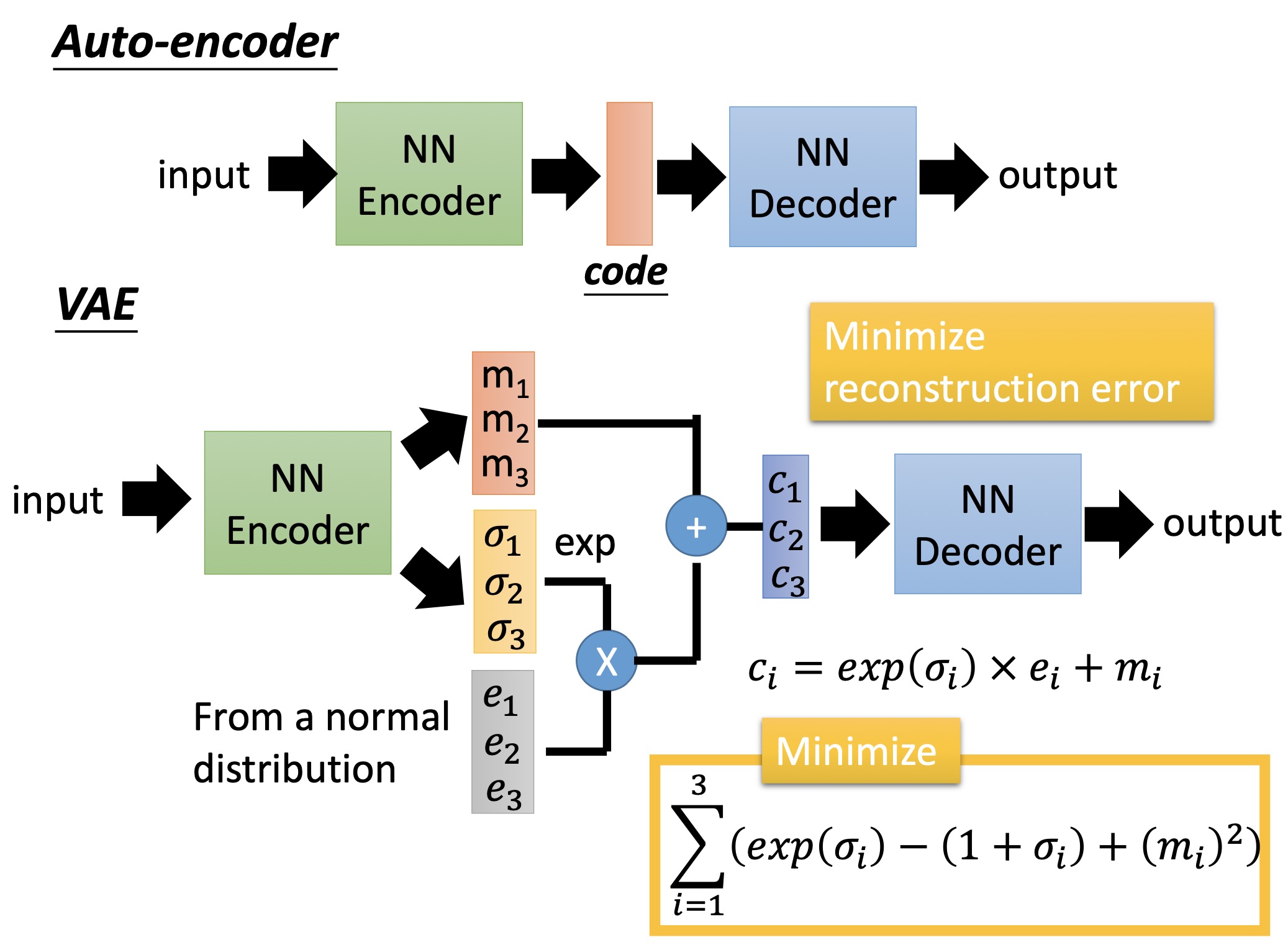
第一个是隐变量$z$。在VAE中，encoder输出两个向量$\sigma$和$m$，然后从标准正态分布中采样一个向量$e$，通过公式$c = exp(\sigma / 2) * e + m$(这个式子图中写错了忘记开根号，$c$相当于隐变量$z$)，再将$c$输入到decoder中。 第二个是loss function。在VAE中，loss为

其中第一项就对应了reconstruction error或者说expected negative log-likelihood，本质上和AE中的loss一样。具体来讲是从encoder输出的distribution即$q_{\theta}(z|x)$中sample出一个$z$(图2中encoder做的事情)，根据这个$z$ decoder会得到一个distribution即$p_{\phi}(x|z)$,我们希望原始数据$x$在该分布中的概率越大越好，这样我们就越有可能sample(重构)出$x$。 而第二项展开来对应了图2中的下面公式。KL距离是衡量两个概率分布的相似程度的函数，一般情况下，我们设定$p(z)$是标准正态分布，$q_{\theta}(z|x)$是一个正态分布，参数由神经网络给出(理论上可以用其它分布表示)。计算推导见后文。

那么VAE这样设计的原理是什么？或者说为什么要和AE有这样的区别？下面从两个角度解释。

从AE的角度来看

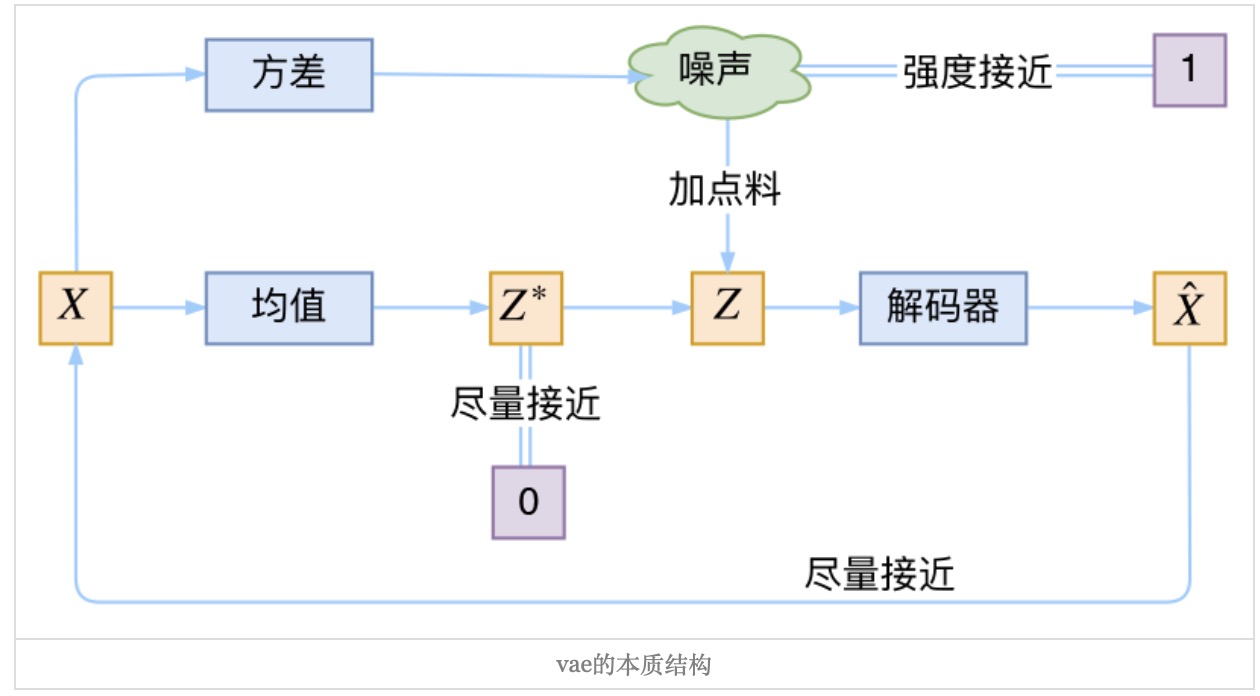
从直觉上看，我们可以将encoder输出的$m$看作是最初的隐变量，加上的部分$exp(\sigma) * e$看作是噪声。这个噪声的分布是 $N(0, exp^{2}(\sigma)$(利用性质：如果$X \sim N(\mu, \sigma^{2})$，那么$aX+b \sim N(a\mu+b, (a\sigma)^2)$)。如果仅仅加上了噪声会出现问题。噪声增加了重构的难度，所以模型会趋向于让噪声的方差为0，这样噪声就失去了随机性(如果正态分布的方差为0，则仅在均值的地方概率为1，其它为0)，也就失去了噪声的意义。说白了，模型会慢慢退化成普通的Auto-Encoder，噪声不再起作用。

所以在loss中增加了一项KL距离，希望$q_{\theta}(z|x)$向$p(z)$也就是标准正态分布看齐，这样我们就可以从标准正态分布中采样$z$来生成我们想要的东西(传统的AE中，$z$的分布未知，对于相似的图片，它们的隐变量表示可能是截然不同的，没有意义的。所以我们很难控制$z$去做有效的生成)。具体来看展开的loss公式，$m^{2}$希望$m$趋向于0，也就是均值为0，也可以看作是$m$的L2正则项。而$exp(\sigma) - (1 + \sigma)$这个loss仅在$\sigma=0$时有最小值0，所以希望$\sigma$趋向于0，也就是噪声的方差趋向于1。

综上所述，VAE中对$z$增加了高斯噪声，使得模型更具有鲁棒性和泛化性；同时在loss中增加了KL距离，使得噪声的方差趋向为1，以及让$z$的均值为0。这样做一是为了让噪声不失效，同时也让我们更容易采样$z$来做生成(参考视频讲解例子)。

从生成模型的角度看

我们的目标是对原始数据进行建模，也就是找到一个概率分布$P(x)$。为此我们引入一个隐变量$z$，它内在的决定了会生成什么$x$，所以有$P(x) = \int P(x|z)P(z) dz$。一般来说$P(x|z)$就是decoder的output。P(z)我们可以假设为标准正态分布。 但这样做其实是不方便的，因为对于每一个从$P(z)$采样出来的$z$我们无从知道它对应哪个$x$。

所以我们考虑先从后验证概率$P(z|x)$中得到$z$，对于不同的x都有其专属的$P(z|x)$，这样就能知道该还原为哪个$x$。而真实的$P(z|x)$又无从可知。 这里用到了变分推断的思想：用一个比较简单的分布$q(z|x)$去逼近真实的分布$P(z|x)$，也就是最小化两者之间的距离。我们用KL距离来衡量这种关系，根据定义得到如下公式:

根据贝叶斯公式：

注意到$P(x)$和$z$无关，所以可以拿到期望外面，所以又有:

所以可以得到最终的公式：

式子左侧为$x$的log-likelihood，右侧有三项；第一项就是最开始我们要最小化的目标，右侧两项就是在上文提到的loss的相反数, 称之为Evidence Lower BOund(ELBO)，因为$KL>=0$，所以$logP(x)>= ELBO$。注意式子里有两个需要优化的参数，一个是$q(z|x)$即encoder，另一个是$P(x|z)$即decoder。而$q(z|x)$和$P(x)$是没有关系的，也就是说我们调整$q(z|x)$使得ELBO不断变大，而$logP(x)$不变，那么等价于让$KL[q(z|x)||P(z|x)]$越来越小，ELBO会趋向于等于$logP(x)$，这个时候再调整$P(x|z)$会使得$logP(x)$和ELBO同时变大（最大似然估计）。

KL距离loss推导

一般情况下我们考虑各个分量独立，所以只推导一元正态分布的情况。

括号中中第一项和$x$无关，容易得到是$-log\sigma^{2}$。第二项为正态分布的二阶矩，推导如下:

第三项可以化作标准正态分布的二阶矩，同理可以算出。

所以最终得到